Problème géométrique à plusieurs solutions du collège au lycée (5ème, 2nde, 1ère S et TS) à propos de l'alignement de 3 points.

télécharger la prépartion en version pdf

Retour au menu

Exercice de géométrie à plusieurs solutions pour préparer l'épreuve d'oral II du CAPES de mathématiques

Date de création: le samedi 8 mars 2008.

Date de la dernière mise à jour: le mercredi 26 mars 2008.

Auteur: Frédéric Rival

Énoncé:

Construire un carré indirect ABCD.

Construire deux triangles équilatéraux directs DCE et BCF.

Créé avec CaRMetal.

Démontrer que les points A, E, et F sont alignés.

Solution n°1:

Niveau: 5^ième / 1^èreS

Outil: Angles géométriques en degré / Angles orientés en radian

ABCD est un carré, et BCF et EDC sont des triangles équilatéraux, donc tous les segments de ces figures sont de même longueur.

ABCD est un carré, donc = .

DCE est un triangle équilatéral donc = .

D'où = – = = . Donc = + = = car BCF est un triangle équilatéral.

De plus, EC = CF donc ECF est un triangle rectangle isocèle en C.

Ainsi = .

= car DEC est un triangle équilatérale.

= – = = .

ADE est un triangle isocèle en D, donc

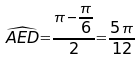
Ainsi, = + + = + + = = .

D'où les points A, E et F sont alignés.

Solution n°2:

Niveau: 1^ère S

Outil: rotation

Aide: Construire le triangle équilatéral ACA'

ou le point A' par la rotation de centre C et d'angle du point A.

Créé avec CaRMetal.

On note A' le point image de A par la rotation de centre C et d'angle .

ACA' est un triangle équilatéral, donc A' appartient à la médiatrice de [AC].

De plus, [BD] est la diagonale du carré ABCD, donc B et D appartiennent à la médiatrice de [AC], d'où A', B, et D sont trois points alignés.

EDC est un triangle équilatéral donc D est l'image de E par la rotation de centre C et d'angle .

BCF est un triangle équilatéral donc B est l'image de F par la rotation de centre C et d'angle .

Comme les points A', B et D sont alignés, et une rotation conserve l'alignement, les points A, E, et F sont alignés.

Solution n°3:

Niveau: T^al S

Outil: complexe

Propriété: Si le point M' d'affixe z' est l'image du point M d'affixe z par la rotation de centre  d'affixe  et d'angle , alors .

Démonstration:

Le point M' d'affixe z' est l'image du point M d'affixe z par la rotation de centre  d'affixe  et d'angle , donc:

Si M≠ i.e. z≠ , alors (,) ≡  (2) et M=M'

donc arg ≡  (2) et |z–| = |z'–| i.e. ||=1.

Ainsi on a donc .

Si M=, alors M'=, donc z= et z'= et l'égalité précédente est toujours vérifiée. En effet, .

cqfd

On considère le repère orthogonal direct (D, , ).

L'affixe de A est i.

L'affixe de E est car E est l'image de C d'affixe 1 par la rotation de centre D et d'angle .

L'affixe de F est car F est l'image de C d'affixe 1 par la rotation de centre B et d'angle .

L'affixe de est .

L'affixe de est .

D'où , donc et sont colinéaires, c'est-à-dire A, E, et F sont trois points alignés.

Solution n°4:

Niveau: 1^ère S

Outil: vecteur

Créé avec CaRMetal.

L'objectif est de calculer le produit scalaire: et de montrer qu'il égal à .

= (+).(+) =

= + + + =

= =

= AB² .

car (, )=(, )+(, )=

Dans le triangle ECF isocèle et rectangle en C, d'après le théorème de Pythagore, on obtient: EF²=EC²+CF²=2AB² donc EF = AB

D'après le théorème d'Al-Kashi, dans le triangle AED, on obtient:

AE² = AD²+DE²â€“2ADxEDcos() = 2AB² (1–) donc AE = AB

Ainsi, AExEF = AB².

On a donc car et

D'où =AB² =AB²=AExEF donc cos(, )=1

donc (, ) ≡ 0 (). Ainsi A, E et F sont trois points alignés.

Solution n°5:

Niveau: 1^ère S

Outil: vecteur (orthogonalité)

On construit le carré direct ECFG.

Démontrons que les droites (AE) et (CG) sont perpendiculaires.

Créé avec CaRMetal.

Calculons .

= + = – + car donc .

Une diagonale du carré ABCD et ECFG vaut AB, d'où:

= –2AB² + AB² = 0 donc (AE) ⊥ (CG).

De plus, (EF) ⊥ (CG) car les diagonales d'un carré sont perpendiculaires.

Donc (EF) // (AE), donc le points A, E et F sont alignés.

Retour au menu